Intro
大三上的后半个学期接触到GAN之后,突然开始对深度学习开始感兴趣,自己也开始多多少少了解了点相关的知识,玩了点现成的代码,甚至想过接触一下CV和计算摄影的相关领域。后来发现自己的脑子似乎不太支持自己去深入研究这些东西,于是还是决定把它当做一个工具,自己蛮学一学。
大三下DM的大作业是:在ML和DL领域选择一种算法,实现具体应用,并进行优化。优化算法这种事情我们显然是搞不来,于是选择在研究方法上进行创新。(虽然最后创了个我到现在还觉得很离谱的方法出来)借此机会,总算是开始独立使用PyTorch搭建神经网络并进行调参。
所以最开始,还是先来回顾一下一个最基本的BP神经网络搭建的过程。本文侧重于训练的过程与PyTorch的使用上,而非BP神经网络的详细原理。之后有有机会复习ML算法的话再聊聊吧(怎么又给自己挖坑了)
在学校借了一本PyTorch的书,虽然有点老但是也还算可以凑活着看。在9月份还书之前慢慢啃一点吧。
Content
- 构建一个神经网络
- 训练参数的准备
- 训练数据的准备
- 训练过程的实现
- 梯度下降的优化
- 最后的代码包装
构建一个神经网络
在Torch中定义网络是一件很简单的事情,只需要用到torch.nn中的 Sequential() 便可以定义一个网络中每一层的具体类型与输入输出。这里以一个简单的三层神经网络为例,包含线性的输入与输出层,以及一个使用ReLU作为激活函数的隐层。Torch囊括了主流的激活函数,如Sigmoid, tanh和RuLU等。通常,为了更快的收敛,我们会在隐层使用RuLU函数。
model = torch.nn.Sequential(
torch.nn.Linear(input_data, hidden_layer),
torch.nn.ReLU(),
torch.nn.Linear(hidden_layer, output_data)
)
|
这里我们将输入节点个数(也就是特征个数)设为1个,隐层节点个数设为10个,最后输出的节点个数为1个:
input_layer = 1
hidden_layer = 10
output_layer = 1
|
这样我们就得到了一个复杂度非常低的网络。低到离谱。
节点的个数是影响网络性能的参数之一。对于输入输出层,其节点个数往往由我们的数据决定;对于隐层,我们通常可以根据以下公式来确定其个数:
$$
(input + ouput)^2 + radn(0,10)
$$
接下来,我们需要定义这个网络的损失函数。torch.nn中支持的损失函数类型有MSELoss, L1Loss和CrossEntropyLoss等,各自适用于处理不同类型的问题。可以在这里找到更多详细的信息:pytorch中常用的损失函数用法说明 | w3c笔记 (w3cschool.cn)。当然去官方的Document找找看肯定是更完整准确的。
这里我们先以MSE作为我们的损失函数:
loss_fn = torch.nn.MSELoss()
|
之后将预测值与实际值传入即可计算损失:
loss = loss_fn(y_pred, y)
|
至此,一个神经网络的基本框架搭建完毕,下一步我们便可以开始为训练做准备。以下是第一部分的完整代码:
import torch
input_data = 1
hidden_layer = 10
output_data = 1
model = torch.nn.Sequential(
torch.nn.Linear(input_layer, hidden_layer),
torch.nn.ReLU(),
torch.nn.Linear(hidden_layer, output_layer)
)
loss_fn = torch.nn.MSELoss()
|
训练参数的准备
基于BPNN的原理,我们需要在训练时完成误差的计算,并根据我们定义的学习率,来控制每一次训练中梯度下降的步长。学习率的控制是一门很复杂的学问,不过一般来说,只要不出现步子迈大了收敛不了的情况就行,但是过小的学习率也会导致收敛过慢。
这里我们定义学习率为1e-4:
训练时,Batch(批)与Epoch(次)也是调起来很玄学的两个参数,影响着训练时间与训练结果的准确性。当整个训练集经过网络处理一次后,我们将这个过程成为一个epoch;由于一个epoch中处理样本可能过于庞大,我们需要将其分为多个小块,也就是batches. 每个batch中的内容从训练集中随机抽取,使用小部分样本对模型权重新进更新。训练一个batch的过程,就是我们常听的“一次Iteration(迭代)”。
那么Epoch和Batch是如何影响训练结果的呢?
Batch size主要决定了收敛速度与随机梯度的噪声,太大不好,太小也不好。太小会延缓训练时间,并且导致过拟合;太大会导致梯度下降得不够到位,误差过大,同时占用大量的内存。(曾经在尝试玩GAN的时候经常因为batch太大炸显存)所以需要经过多次尝试来确定batch size.
Epoch主要影响拟合的程度。使用多个Epoch的原因在于,仅有一次完整的训练往往会导致欠拟合,但过多的Epoch也会导致过拟合。
那么,究竟要怎么取到合适的Batch size和epoch呢?
其实没有正确的答案,因为对于不同的训练集,我们使用的参数往往是不同的。通常来说,batch size一般不会低于16,我们可以根据这个限制,与样本的大小,去确定batch size;对于epoch的数量,emmm…反正我是自己感受的hhhhh,用很大的值试一试,很小的的值也试一试,根据训练的情况去选择一个合适的值。
反正只要避免出问题就好了。真的很玄学。
代码实现上,epoch只要用for循环来控制就好了,batch则需要写一个专门用来分割的小东西,以将划分好的batches返回进训练过程中:
def batch_loader(x, y, batch_size=64):
"""
Args:
x: 训练数据 Tensor or ndarray
y: 训练数据标签 Tensor or ndarray
batch_size: Mini-batch 大小
Returns:
x_batch, y_batch: mini-batch 数据对
"""
data_size = x.shape[0]
permutation = np.random.permutation(data_size)
for i in range(0, data_size, batch_size):
batch_permutation = permutation[i: i+batch_size]
yield x[batch_permutation], y[batch_permutation]
|
(CtrlC CtrlV来的)
Epoch我们暂定给1000个吧,batch size给个100看看.
num_epoch = 1000
batch_size = 100
|
训练数据的准备
正常来说,我们需要将数据导入,并进行训练集与测试集的分割。这里为了省点事情,我们就暂且不进行划分。我们使用以下公式,随机生成一组0~1之间的随机数作为Y,并引入一些噪声:
import numpy as np
def F(x):
return 1 / (1 + np.exp(x))
X_BOUND = [-10, 10]
data_length = 1000
noise = 0.1
x = X_BOUND[0] + (X_BOUND[1]-X_BOUND[0]) * np.random.rand(data_length)
y = F(x) + noise * np.random.rand(data_length)
|
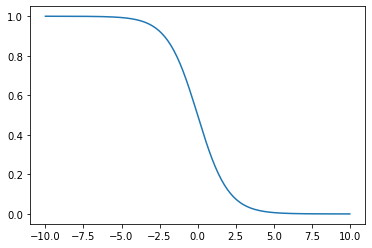
接着,我们需要将其包装为tensor(张量):
x_tensor = torch.from_numpy(x).unsqueeze_(-1).float()
y_tensor = torch.from_numpy(y).unsqueeze_(-1).float()
|
正常来说,这一步需要做的事情很多:如果是现实中的数据,我们还需要进行归一化的处理,以消除各变量之间量级差距所带来的误差;如果是分类变量,我们需要将每一种分类独立出来,作为一个0/1的dummy变量,等等。之后我会在下一篇DL文章中,用我当时大作业的数据进行演示。
训练过程的实现
刚刚提到,我们将会用for循环来实现对epoches的训练,因此我们需要将具体的训练过程装进这个for中。训练一个BP神经网络的流程大致包含了误差计算、反向传播与梯度计算,更新权重这几个步骤。这些步骤都可以很轻易的用PyTorch实现。
首先,我们需要建立一个用于记录误差的列表,以便我们在每次迭代后能够记录当前的损失,并在训练完一个epoch之后进行平均,供我们评估模型的性能。当然,在这之后,需要清空这个列表,开始新的一轮训练。
这是一个大框架:
loss_list = []
for e in range(num_epoch):
loss_list.clear()
for i, (x_batch, y_batch) in enumerate(batch_loader(x_tensor, y_tensor, batch_size)):
pass
loss_list.append(
print(np.mean(loss_list))
|
接下来,我们需要将具体的训练内容放进for中。
第一件事情,当然是将x输入网络中,进行预测。
接着,我们用刚刚提到过的那句代码计算损失,并执行反向传播:
loss = loss_fn(y_pred, y_batch)
model.zero_grad()
loss.backward()
|
要想实现梯度下降并更新权重,我们需要从模型中提取参数,并执行更新的公式:
for param in model.parameters():
param.data -= param.grad.data * lr
|
紧接着记录一下本次迭代的误差:
loss_list.append(loss.item())
|
在训练完一个epoch之后,计算一下MSE:
至此,我们已经初步搭建好训练的逻辑与步骤了。以下是完整代码:
import numpy as np
from matplotlib import pyplot as plt
def batch_loader(x, y, batch_size=64):
"""
Args:
x: 训练数据 Tensor or ndarray
y: 训练数据标签 Tensor or ndarray
batch_size: Mini-batch 大小
Returns:
x_batch, y_batch: mini-batch 数据对
"""
data_size = x.shape[0]
permutation = np.random.permutation(data_size)
for i in range(0, data_size, batch_size):
batch_permutation = permutation[i: i+batch_size]
yield x[batch_permutation], y[batch_permutation]
def F(x):
return 1 / (1 + np.exp(x))
X_BOUND = [-10, 10]
data_length = 1000
noise = 0.1
x = X_BOUND[0] + (X_BOUND[1]-X_BOUND[0]) * np.random.rand(data_length)
y = F(x) + noise * np.random.rand(data_length)
x_tensor = torch.from_numpy(x).unsqueeze_(-1).float()
y_tensor = torch.from_numpy(y).unsqueeze_(-1).float()
input_layer = 1
hidden_layer = 10
output_layer = 1
model = torch.nn.Sequential(
torch.nn.Linear(input_layer, hidden_layer),
torch.nn.ReLU(),
torch.nn.Linear(hidden_layer, output_layer)
)
loss_fn = torch.nn.MSELoss()
num_epoch = 1000
batch_size = 100
lr = 1e-3
loss_list = []
for e in range(num_epoch):
loss_list.clear()
for i, (x_batch, y_batch) in enumerate(batch_loader(x_tensor, y_tensor, batch_size)):
y_pred = model(x_batch)
loss = loss_fn(y_pred, y_batch)
model.zero_grad()
loss.backward()
for param in model.parameters():
param.data -= param.grad.data * lr
loss_list.append(loss.item())
print('batch {} loss {}'.format(i+1, loss.item()), end='\r')
print('epoch {} loss {}'.format(e+1, np.mean(loss_list)))
|
训练完毕之后,我们可以通过输出的结果看到误差不断减少的过程。如果想直观地看到训练成果,我们可以将原数据集传入训练完毕的模型中进行预测,并将原数据的曲线和预测结果的曲线一起plot出来进行对比:
x_axis = np.linspace(*X_BOUND, 200)
plt.plot(x_axis, F(x_axis))
plt.scatter(x, np.squeeze(
model(x_tensor).detach().cpu().numpy(), -1), color='r')
plt.show()
|
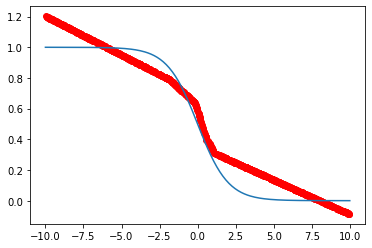
红色曲线为预测结果,蓝色曲线为原数据,可以看到还是很接近的。如果我们增加epoch、提高learning rate,或是增大batch size,训练误差也会随之减小。
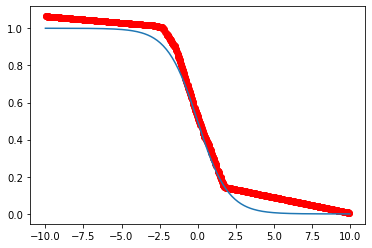
当然,这只是训练误差,并不代表模型真正的预测性能。想要正确评判模型的预测性能,还是需要引入测试集进行验证。之后再说啦~
梯度下降的优化
某种意义上来说,BP神经网络是一种局部搜索算法,这使他在训练过程中不可避免地会陷入局部最优,从而导致训练结果不佳。此外,收敛速度慢也是它的缺点之一。为了解决这些问题,我们可以从两方面入手:优化初始权重 ,与优化梯度下降的算法。前者通常与在GA、PSO等算法的辅助下进行,之后有机会也会展示一下具体的做法;后者则可以利用PyTorch自带的Optimizer (torch.optim) 进行优化。torch.optim中包含了多种优化算法,如Adam, AdamW 和 Adamax等,当然也包含了我们刚刚的随机梯度下降方法SGD。若要使用torch.optim, 我们需要确定一种优化算法,然后将模型的参数与学习率传进去:
optimizer = torch.optim.SGD(model.parameters(), lr=lr)
|
同时,将刚刚训练过程中的部分代码进行替换:
optimizer.zero_grad()
'''
for param in model.parameters():
param.data -= param.grad.data * lr
'''
optimizer.step()
|
再次执行代码,我们可以得到一个和之前性能几乎相同的模型。
如果此时我们将SGD换为Adam,并依然使用Epoch = 1000, Batch_size = 100, Learning_rate = 1e-3这套参数:
optimizer = torch.optim.Adam(model.parameters(), lr=lr)
|
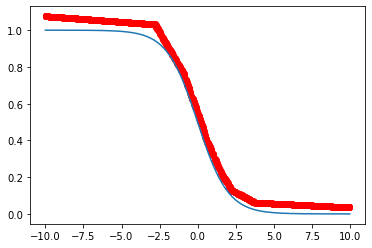
一步到位。
即使此时我们将Learning_rate减小到1e-4:
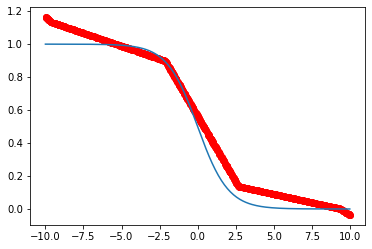
结果还是会比刚刚SGD好不少的。
最后的代码包装
至此,我们已经得到了一个最简单的神经网络模型,并初步体验了调参的……呃用什么形容词词好呢……反正就是一件神奇又折磨人的事情……
接来下我们要做的,就是把我们的代码包装成一个类,方便我们之后的调用。直接上代码:
import torch
import numpy as np
class BPNN():
def __init__(self, input_layer, hidden_layer, output_layer, x, y, epoch, batch_size, lr, log):
self.input_layer = input_layer
self.hidden_layer = hidden_layer
self.output_layer = output_layer
self.x = x
self.y = y
self.epoch = epoch
self.batch_size = batch_size
self.lr = lr
self.log = log
def batch_loader(self, x, y, batch_size=64):
data_size = x.shape[0]
permutation = np.random.permutation(data_size)
for i in range(0, data_size, batch_size):
batch_permutation = permutation[i: i + batch_size]
yield x[batch_permutation], y[batch_permutation]
def build_model(self):
input_layer = self.input_layer
hidden_layer = self.hidden_layer
output_layer = self.output_layer
model = torch.nn.Sequential(
torch.nn.Linear(input_layer, hidden_layer),
torch.nn.ReLU(),
torch.nn.Linear(hidden_layer, output_layer)
)
loss_fn = torch.nn.MSELoss()
return model, loss_fn
def train_model(self):
num_epoch = self.epoch
batch_size = self.batch_size
lr = self.lr
x = self.x
y = self.y
model, loss_fn = self.build_model()
optimizer = torch.optim.Adam(model.parameters(), lr=lr)
loss_list = []
for e in range(num_epoch):
loss_list.clear()
for i, (x_batch, y_batch) in enumerate(self.batch_loader(x, y, batch_size)):
y_pred = model(x_batch)
loss = loss_fn(y_pred, y_batch)
optimizer.zero_grad()
loss.backward()
optimizer.step()
loss_list.append(loss.item())
if self.log:
print('batch {} loss {}'.format(i + 1, loss.item()), end='\r')
if self.log:
print('epoch {} loss {}'.format(e + 1, np.mean(loss_list)))
return model, np.mean(loss_list)
|
将以上代码保存为BPNN.py, 然后在同一目录下新建一个.py文件,调用BPNN.py写好主程序:
from BPNN import BPNN
import torch
import numpy as np
from matplotlib import pyplot as plt
def F(x):
return 1 / (1 + np.exp(x))
if __name__ == "__main__":
X_BOUND = [-10, 10]
data_length = 1000
noise = 0.1
x = X_BOUND[0] + (X_BOUND[1] - X_BOUND[0]) * np.random.rand(data_length)
y = F(x) + noise * np.random.rand(data_length)
x_tensor = torch.from_numpy(x).unsqueeze_(-1).float()
y_tensor = torch.from_numpy(y).unsqueeze_(-1).float()
MyBPNN = BPNN(input_layer=1, hidden_layer=10, output_layer=1,
x=x_tensor, y=y_tensor,
epoch=1000, batch_size=100, lr=1e-4,
log=True)
model, loss = MyBPNN.train_model()
print('MSE: ', loss)
x_axis = np.linspace(*X_BOUND, 200)
plt.plot(x_axis, F(x_axis))
plt.scatter(x, np.squeeze(
model(x_tensor).detach().cpu().numpy(), -1), color='r')
plt.show()
|
挖坑
BP神经网路部分的下一篇文章会将以上神经网络应用在空气质量预测上(数据源:Beijing Multi-Site Air-Quality Data - UCI Machine Learning Repository),加入数据的预处理、训练集测试集的划分,以及最后的验证上。
下下篇文章则会将网络与GA、PSO算法结合(使用 scikit-opt),实现对神经网络性能的进一步优化。
References
PyTorch 神经网络 - PyTorch官方教程中文版 (pytorch123.com)
cattidea/bp-ga-pytorch: bp-ga algorithm implemented by pytorch (github.com)
(20条消息) 训练神经网络 | 三个基本概念:Epoch, Batch, Iteration_OnlyCoding…的博客-CSDN博客